Линейное программирование графический метод примеры решения. Графический метод решения задач линейного программирования

f = –х 1 + 5х 2 ¾> min ;

4х 1+ 3х 2 £ 24,

х 1– 10х 2 £ 0,

8х 1– 3х 2 ³ 0,

5х 1+ 3х 2 ³ 15,

х 1³0, х 2³ 0. (1)

Совокупность переменных хj , удовлетворяющих условию (1), называется областью допустимых решений. Допустимое решение, обращающее целевую функцию в min или max , называется оптимальным. Для его определения необходимо построить область допустимых решений (область определения). Так как в условии задачи заданы две переменные, то область допустимых решений находится на плоскости х 10х 2. Каждое неравенство (1) определяет полуплоскость, а равенство – прямую. Для построения полуплоскости необходимо найти ее границу и установить, с какой стороны от нее лежит искомая полуплоскость. Перепишем условия (1) в виде равенств (2) и пронумеруем их.

4х 1+ 3х 2	=	24 (I ),
х 1– 10х 2	=	0 (II ),
8х 1– 3х 2	=	0 (III ),
5х 1+ 3х 2	=	15 (IV ).	(2)

Введем систему координат х 10х 2 и построим последовательно эти прямые – границы полуплоскостей. Для построения прямой на плоскости необходимо определить любые две точки, лежащие на этой прямой. Если прямая пересекает оси 0х 1и 0х 2, то можно найти координаты точек ее пересечения с осями координат. Определим координаты пересечения прямой (I ) с осью 0х 1: х 1=0; Þ 3х 2= 24; Þ х 2= 8. Соответственно определим координаты второй точки пересечения первой прямой с осью 0х 2: х 2=0; Þ 4х 1= 24; Þ х 1= 6. Следовательно, точки пересечения прямой (I ) с осями координат равны (0,8) и (6,0). Построим эту прямую (рис. 1).

Определим полуплоскость. Для этого подставим в первое неравенство (1) координаты любой точки, не лежащей на данной прямой, например (0,0). Тогда из первого условия следует: 4×0+3×0 £24, значит, неравенство справедливо, откуда следует, что полуплоскость лежит с той стороны прямой, где находится точка с координатами (0,0).

Аналогичным образом строятся и другие полуплоскости. Необходимо учесть, что прямые (II) и (III) проходят через начало координат, т.е. точку (0,0). Координаты второй точки желательно брать пропорционально коэффициентам в уравнении искомой прямой. Например, для второй прямой – точки (0,0) и (10,1), а для третьей – (0,0) и (3,8). После построения всех полуплоскостей область допустимых решений примет следующий вид (рис. 3):

Целевая функция f определяет на плоскости прямую, которая должна проходить через точку или сторону многоугольника и иметь наименьшее значение. Построим направляющий вектор для этой прямой. Данный вектор перпендикулярен искомой прямой, и его направление всегда определяет максимум целевой функции. Противоположное направление вектора определяет минимум. Обозначим этот вектор через . Он проходит через точку (0,0) и (–1,5). Координаты второй точки берут из коэффициентов целевой функции и с их помощью определяют направление вектора. Перпендикулярно ему построим прямую –х 1+ 5х 2=0. Как было сказано выше, вектор всегда показывает направление возрастания значения целевой функции (max ) , противоположный ему вектор –– направление убывания значения целевой функции (min ). Перемещаем прямую –х 1+5х 2=0 по области определения параллельно самой себе в направлении min . Целевая функция f достигнет своего минимального значения в точке С (рис. 4).

Оптимальному решению задачи (1) соответствует точка С , которая лежит на пересечении прямых (I ) и (II ):

4х 1+ 3х 2= 24;

х 1– 10х 2= 0.

Для решения данной системы уравнений умножить второе уравнение на 4 и сложить соответственно по элементам с 1-м уравнением:

4х 1+ 3х 2 = 24;

4х 1– 40х 2 = 0.

Вычтем из первого уравнения второе, получим: 43х2= 24 Þ х 2= 0,56.

Подставив найденное значение х 2во второе уравнение, получим:

х 1= 10х 2Þ х 1=5,6. Подставив координаты точки С в целевую функцию, получим следующий результат:

f min = – 5,6 + 5×0,56 = – 2,8.

Окончательный результат задачи запишем в следующем виде:

х 1= 5,6, х 2= 0,56;f min = – 2,8.

Решение данного примера на ПЭВМ осуществляется программным комплексом «Блок-3». С его помощью производятся ввод, решение и вывод результативной информации на внешний носитель. Простота и доступность комплекса позволит без труда освоить его и применять на практике.

Задача № 1.1.2.

f = 2х 1+ 3х 2 ¾> max;

2х 1+ 3х 2 £ 12,

2х 1– 5х 2 £ 0,

7х 1– 2х2³ 0,

х 1, х 2³ 0. (3)

Определения и построение области допустимых решений аналогичны заданию 1.1.1. Окончательный вид области допустимых решений представлен на рис. 5 многоугольником АВС (точка А совпадает с точкой 0).

Очевидно, что прямая, определяющая целевую функцию, совпадает с прямой, образующей сторону многоугольника ВС . Отсюда следует, что решением данной ЭММ являются точки, лежащие на стороне ВС много-

угольника АВС . Для записи решения ЭММ необходимо найти координату x 1B – точки В и x 1C – точки С . Определив их, мы сможем найти отрезок, лежащий на оси 0x 1(рис. 6).

Координаты точки В – x1B определяются в результате пересечения прямых 2х 1+ 3х 2 = 12 и 7х 1– 2х 2 = 0. Для этого необходимо решить систему уравнений:

2х 1+ 3х 2= 12 ´ 2 Þ 4х 1+ 6х 2= 24;

7х 1– 2х 2= 0 ´ 3 Þ 21х 1– 6х2= 0.

Сложив два последних уравнения, получим: 25х 1=24, х 1=0,96. Из этого следует, что x 1B =0,96. Координата точки С – x 1C определяется в результате пересечения прямых 2х 1+ 3х 2=12 и 2х 1–5х 2=0. Решим систему уравнений:

2х 1+ 3х 2= 12 ´ 5 Þ 10х 1+ 15х 2= 60;

2х 1– 5х 2= 0 ´ 3 Þ 6х 1 – 15х 2= 0.

Сложив два последних уравнения, получим: 16х 1= 60, х 1= 3,75, откуда следует, что x 1C = 3,75.

Значение целевой функции для данной ЭММ равно 12 (так как уравнение прямой, на которой определен отрезок ВС – 2х 1+3х 2= 12).

Таким образом, ответ данной задачи:

x 1Î[x 1B ; x 1C ] Þ x 1Î;

2х 1+ 3х 2=12 Þ 3х 2= 12 – 2х 1Þ х 2= (12 – 2х 1)/3.

Полный ответ данного примера запишется в следующем виде:

x 1Î; x 2= (12 – 2х 1)/3; f max = 12.

Задача № 1.1.3.

f = 2х 1+ 3х 2 ¾> max;

2х 1+ 3х 2 ³ 12,

2х 1– 5х 2 £ 0,

7х 1– 2х 2³ 0,

х 1, х 2 ³0. (4)

Используя схему построения области допустимых решений задач 1.1.1–1.1.2, получим следующий график (рис. 7):

f = 2х 1+ 3х 2 ¾> max ;

х 1+ х2 £ 2,

2х 1+ 3х 2³ 12,

2х 1– 5х 2£ 0,

7х 1– 2х 2³ 0,

х 1, х 2³ 0. (5)

Используя график задачи 1.1.3 и достроив первую полуплоскость х 1+х2£ 2, получим область определения, показанную на рис. 8.

Из графика (рис. 8) видно, что для данной ЭММ области допустимых решений нет. Ответ: нет области допустимых решений.

Задача № 1.1.5.

f = – х 1+ 5х 2 ¾> min;

10х 1+ 3х 2£ 30,

10х 1+ 5х 2³ 50,

2х 1– 6х 2£ 0,

х 1, х 2³ 0. (6)

Область определения ЭММ (6) представлена на рис. 9. Из анализа графика следует, что областью допустимых решений будет являться точка А с координатами (0,10) (10х 1+ 5х 2= 50, х 1= 0, 5х 2= 50, х 2=10). В случае, когда решением ЭММ является единственная точка, целевую функцию можно не строить.

Ответ: x 1= 0; x 2=10; fmin = 0+5×10 = 50.

Таким образом, при решении задач ЭММ ЛП возможны следующие ситуации:

– задача имеет одно оптимальное решение;

– задача имеет бесконечное число оптимальных решений;

– задача не имеет оптимального решения;

– задача не имеет области допустимых решений.

На практике ЭММ ЛП не имеет решений только в том случае, если некорректна постановка задачи.

Как показывает опыт разработки ЭММ, основная сложность состоит в описании экономико-технологических процессов в модели и выборе критерия оптимизации. Отсюда следует, что необходимо точно определить нормативные параметры. Это в свою очередь требует поставленного учета и анализа на исследуемом объекте. В то же время особое значение в составлении модели приобретает уровень подготовки специалиста. От его умения выявить основные звенья технологического процесса, определить этапы решения задачи и сформулировать цели исследования будет зависеть и качество решения данной проблемы.

Задача № 1.1.6.

Предприятие может организовать производство своей продукции двумя способами. При первом способе предприятие за месяц выпускает C 1 тыс. изделий, при втором – C 2 тыс. изделий. Расход производственных, людских ресурсов, амортизация оборудования и ограничения ресурсов, приведены ниже в таблице.

Сколько месяцев должно работать предприятие, каким способом организовать производство, чтобы обеспечить максимальный выпуск продукции.

1) Решить графическим способом;

2) Решить на базе комплекса «Блок-3»;

3) Симплекс-методом.

Задача. Решить графически задачу линейного программирования, определив экстремальное значение целевой функции:

при ограничениях

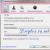
Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).

Построим уравнение 3x 1 +x 2 = 9 по двум точкам .
Для нахождения первой точки приравниваем x 1 = 0. Находим x 2 = 9. Для нахождения второй точки приравниваем x 2 = 0. Находим x 1 = 3. Соединяем точку (0;9) с (3;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 3 . 0 + 1 . 0 - 9 ≤ 0, т.е. 3x 1 +x 2 - 9≥ 0 в полуплоскости выше прямой.
Построим уравнение x 1 +2x 2 = 8 по двум точкам .
Для нахождения первой точки приравниваем x 1 = 0. Находим x 2 = 4. Для нахождения второй точки приравниваем x 2 = 0. Находим x 1 = 8. Соединяем точку (0;4) с (8;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 1 . 0 + 2 . 0 - 8 ≤ 0, т.е. x 1 +2x 2 - 8≥ 0 в полуплоскости выше прямой.
Построим уравнение x 1 +x 2 = 8 по двум точкам .
Для нахождения первой точки приравниваем x 1 = 0. Находим x 2 = 8. Для нахождения второй точки приравниваем x 2 = 0. Находим x 1 = 8. Соединяем точку (0;8) с (8;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 1 . 0 + 1 . 0 - 8 ≤ 0, т.е. x 1 +x 2 - 8≤ 0 в полуплоскости ниже прямой.

Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.
Обозначим границы области многоугольника решений.

Проверить правильность построения графиков функций можно с помощью калькулятора

Рассмотрим целевую функцию задачи F = 4x 1 +6x 2 → min.
Построим прямую, отвечающую значению функции F = 0: F = 4x 1 +6x 2 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление минимизации F(X). Начало вектора - точка (0; 0), конец - точка (4; 6). Будем двигать эту прямую параллельным образом. Поскольку нас интересует минимальное решение, поэтому двигаем прямую до первого касания обозначенной области. На графике эта прямая обозначена пунктирной линией.

Прямая F(x) = 4x 1 +6x 2 пересекает область в точке B. Так как точка B получена в результате пересечения прямых (1) и (2) , то ее координаты удовлетворяют уравнениям этих прямых:
3x 1 +x 2 =9
x 1 +2x 2 =8

Решив систему уравнений, получим: x 1 = 2, x 2 = 3
Откуда найдем минимальное значение целевой функции:
F(X) = 4*2 + 6*3 = 26

Краткая теория

Линейное программирование - раздел математического программирования, применяемый при разработке методов отыскания экстремума линейных функций нескольких переменных при линейных дополнительных ограничениях, налагаемых на переменные. По типу решаемых задач его методы разделяются на универсальные и специальные. С помощью универсальных методов могут решаться любые задачи линейного программирования (ЗЛП). Специальные методы учитывают особенности модели задачи, ее целевой функции и системы ограничений. Особенностью задач линейного программирования является то, что экстремума целевая функция достигает на границе области допустимых решений.

Графический метод решения задач линейного программирования дает возможность наглядно представить их структуру, выявить особенности и открывает пути исследования более сложных свойств. Задачу линейного программирования с двумя переменными всегда можно решить графически. Однако уже в трехмерном пространстве такое решение усложняется, а в пространствах, размерность которых больше трех, графическое решение, вообще говоря, невозможно. Случай двух переменных не имеет особого практического значения, однако его рассмотрение проясняет свойства ограничений ЗЛП, приводит к идее ее решения, делает геометрически наглядными способы решения и пути их практической реализации.

Если ограничения и целевая функция содержит более двух переменных, тогда необходимо (или методом последовательного улучшения решения) - он универсален и им можно решить любую ЗЛП. Для некоторых прикладных задач линейного программирования, таких как , разработаны специальные методы решения.

Пример решения задачи

Условие задачи

Предприятие выпускает два вида продукции: Изделие 1 и Изделие 2. На изготовление единицы Изделия 1 требуется затратить кг сырья первого типа, кг сырья второго типа, кг сырья третьего типа. На изготовление единицы Изделия 2 требуется затратить кг первого типа, сырья второго типа, сырья третьего типа. Производство обеспечено сырьем каждого типа в количестве кг, кг, кг соответственно. Рыночная цена единицы Изделия 1 составляет тыс руб., а единицы Изделия 2 - тыс. руб.

Требуется:

• Построить математическую модель задачи.
• Составить план производства изделий, обеспечивающий максимальную выручку от их реализации при помощи графического метода решения задачи линейного программирования.

Чтобы решение задачи по линейному программированию было максимально точным и верным, многие недорого заказывают контрольную работу на этом сайте. Подробно (как оставить заявку, цены, сроки, способы оплаты) можно почитать на странице Купить контрольную работу по линейному программированию...

Решение задачи

Построение модели

Через и обозначим количество выпускаемых изделий 1-го и 2-го типа.

Тогда ограничения на ресурсы:

Кроме того, по смыслу задачи

Целевая функция экономико-математической модели, выражающая получаемую от реализации выручку:

Получаем следующую экономико-математическую модель:

Построение области допустимых решений

Решим полученную задачу линейного программирования графическим способом:

Для построения области допустимых решений строим в системе координат соответствующие данным ограничениям-неравенствам граничные прямые:

Найдем точки, через которые проходят прямые:

Решением каждого неравенства системы ограничений ЗЛП является полуплоскость, содержащая граничную прямую и расположенная по одну сторону от нее.

Для определения полуплоскости возьмём любую точку, например , не принадлежащую прямой (1), подставим координаты (0;0) в соответствующее неравенство. Т.к. неравенство верно:

Области решений соответствующего 1-го неравенства соответствует левая полуплоскость

Возьмём любую точку, например , не принадлежащую прямой (2), подставим координаты (0;0) в соответствующее неравенство. Т.к. неравенство верно:

Возьмём любую точку, например , не принадлежащую прямой (3), подставим координаты (0;0) в соответствующее неравенство. Т.к. неравенство верно:

Области решений соответствующего 2-го неравенства соответствует левая полуплоскость

Областью допустимых решений является фигура .

Нахождение решения задачи ЛП

Строим вектор , координаты которого пропорциональны коэффициентам целевой функции. Здесь - коэффициент пропорциональности.

Перпендикулярно к построенному вектору проводим линию уровня .

Перемещаем линию уровня в направлении вектора так, чтобы она касалась области допустимых решений в крайней точке. Решением на максимум является точка , координаты которой находим как точку пересечения прямых (2) и (1).

Ответ

Таким образом необходимо выпускать 56 изделий 1-го вида и 64 изделия 2-го вида. При этом выручка от реализации изделий будет максимальна и составит 5104 ден.ед.

Метод графического решения, если задача с двумя переменными имеет линейные ограничения, а целевая функция - квадратичная, подробно рассмотрен здесь
На странице подробно разобрано решение задачи линейного программирования симплексным методом, кроме того, показано построение двойственной задачи линейного программирования и нахождение ее решения по решению прямой задачи.

Транспортная задача и метод потенциалов
Подробно рассмотрена транспортная задача, ее математическая модель и методы решения - нахождение опорного плана методом минимального элемента и поиск оптимального решения методом потенциалов.

Выпуклое программирование - графический метод
Приведен образец решения задачи квадратичного выпуклого программирования графическим методом.

Рассмотрим сначала простейший случай, когда в ЗЛП включены ровно две переменные:

Каждое из неравенств (a)-(b) системы ограничений задачи (3.8) геометрически определяет полуплоскость соответственно с граничными прямыми , Х 1 =0 и Х 2 =0. Каждая из граничных прямых делит плоскость х 1 Ох 2 на две полуплоскости. Все решения исходного неравенства лежат в одной из образованных полуплоскостей (все точки полуплоскости) и, следовательно, при подстановке координат любой ее точки в соответствующее неравенство обращает его в верное тождество. С учетом этого и определяется та полуплоскость, в которой лежат решения неравенства, т.е. путем выбора любой точки из какой-либо полуплоскости и подстановки ее координат в соответствующее неравенство. Если неравенство выполняется для данной точки, то оно выполняется и для любой другой точки из этой же полуплоскости. В противном случае решения неравенства лежат в другой полуплоскости.

В том случае, если система неравенств (a)-(b) совместна, то область её решений есть множество точек, принадлежащих всем указанным полуплоскостям. Так как множество точек пересечения данных полуплоскостей выпуклое, то область допустимых решений задачи (3.8) является выпуклое множество, которое называется многоугольником решений (введённый ранее термин “многогранник решений” обычно употребляется, если n 3). Стороны этого многоугольника лежат на прямых, уравнения которых получаются из исходной системы ограничений заменой знаков неравенств на знаки точных равенств.

Таким образом, исходная ЗЛП состоит в нахождении такой точки многоугольника решений, в которой целевая функция F принимает максимальное (минимальное) значение.

Эта точка существует тогда, когда многоугольник решений не пуст и на нём целевая функция ограничена сверху. При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение. Для определения данной вершины строят линию уровня L: c 1 x 1 +c 2 x 2 =h (где h – некоторая постоянная), перпендикулярную вектору-градиенту и проходящую через многоугольник решений, и передвигают её параллельно вдоль вектора-градиента до тех пор, пока она не пройдёт через последнюю её общую точку пересечения с многоугольником решений (при построении вектора-градиента откладывают точку (с 1 ; с 2) в плоскости х 1 Ох 2 и проводят к ней из начала координат направленный отрезок). Координаты указанной точки и определяют оптимальный план данной задачи.

Суммируя все выше изложенное, приведем алгоритм графического метода решения ЗЛП.

Алгоритм графического метода решения ЗЛП

1. Построить многоугольник решений, задаваемый системой ограничений исходной ЗЛП.

2. Если построенный многоугольник решений – пустое множество, то исходная ЗЛП решений не имеет. В противном случае построить вектор-градиент и провести произвольную линию уровня L, перемещая которую при решении задачи на максимум в направлении вектора (или в обратном направлении для задачи на минимум) определить крайнюю точку многоугольника решений, где и достигается максимум (минимум) целевой функции задачи.

3. Вычислить координаты найденной оптимальной точки , решив систему уравнений двух граничных прямых, пересекающихся в ней.

4. Подстановкой найденного оптимального решения в целевую функцию задачи вычислить оптимальное ее значение, т.е.: .

При графическом построении множества допустимых решений ЗЛП (многоугольника решений) возможны следующие ситуации.

Графический метод решения ЗЛП основан на утверждениях, приведенных в пункте 2.1. Согласно теореме 2, оптимальное решение находится в вершине области допустимых решений и поэтому решить ЗЛП – найти вершину области допустимых решений, координаты которой дают оптимальное значение целевой функции.

Графический метод используют для решения ограниченного класса задач с двумя переменными, иногда с тремя переменными. Надо заметить, что для трех переменных эта область является недостаточно наглядной.

Алгоритм графического метода решения злп

Реализацию графического метода решения ЗЛП рассмотрим на примерах.

Пример 2.2.1. Решить ЗЛП графическим методом:

(2.2.1)

max z =x 1 + 4x 2 (2.2.2)

Решение. Для построения области допустимых решений, которая состоит из пересечения полуплоскостей, соответствующих каждому неравенству системы ограничений (2.2.1), запишем уравнения граничных прямых:

l 1: x 1 + 5x 2 = 5; l 2: x 1 + x 2 = 6; l 3: 7x 1 + x 2 = 7.

l 1 к виду (2.2.3.) разделим обе его части на 5:
. Таким образом, прямаяl 1 отсекает на оси Ох 1 5 единиц, на оси Ох 2 1 единицу. Аналогично имеем для l 2:
иl 3:
.

Для определения полуплоскостей, которые отвечают ограничениям системы (2.2.1), в ограничения нужно подставить координаты какой-либо точки, не лежащей на граничной прямой. Если получим верное неравенство, то все точки из этой полуплоскости являются решениями данного неравенства. В противном случае выбирают другую полуплоскость.

Таким образом, первая и вторая искомые полуплоскости расположены в противоположную сторону от начала координат (0 – 5·0– 5; 7·0 + 07), а вторая – в сторону начала координат (0 + 06). Область допустимых решений на рисунке 2.2.1 заштрихована.

Рисунок 2.2.1 – Область допустимых решений

Для нахождения оптимального плана, который будет находиться в вершине многоугольника решений, нужно построить вектор направлений
=(с 1 ,с 2), который указывает направление наибольшего возрастания целевой функцииz =с 1 х 1 +с 2 х 2 .

В данной задаче вектор направлений
= (1, 4): он начинается в точкеО (0,0) и заканчивается в точкеN (1, 4).

Далее строим прямую, которая проходит через область допустимых решений, перпендикулярно к вектору , и называетсялинией уровня целевой функции. Передвигаем линию уровня в направлении векторав случае максимизации целевой функцииz и в направлении противоположном, в случае минимизацииz , до последнего пересечения с областью допустимых решений. В результате определяется точка или точки, где целевая функция достигает экстремального значения, или устанавливается неограниченность целевой функцииz на множестве решений задачи.

Таким образом, точкой максимума целевой функции z является точкаА пересечения прямыхl 2 иl 3 .

Для вычисления оптимального значения целевой функции z найдем координаты точки А. Поскольку точка А – это точка пересечения прямых l 2 и l 3 , то ее координаты удовлетворяют системе уравнений, составленной из уравнений соответствующих граничных прямых:

Таким образом, точка А имеет координаты x 1 =1/6, x 2 = 35/6.

Для вычисления оптимального значения целевой функции нужно подставить в нее координаты точки А.

Подставив координаты точки А в целевую функцию (2.4), получим

max z = 1/6 + 4·(35/6) = 47/2.

Пример 2.2.2. Построить на плоскости область допустимых решений системы линейных неравенств (2.2.4) и найти наибольшее и наименьшее значения целевой функции (2.2.5):

(2.2.4)

z = –2x 1 –x 2 (2.2.5)

Решение. Для построения области допустимых решений, которая состоит из пересечения полуплоскостей, соответствующих каждому неравенству системы ограничений (2.2.4), запишем уравнения граничных прямых:

l 1: 4x 1 – x 2 = 0; l 2: x 1 + 3x 2 = 6; l 3: x 1 – 3x 2 = 6; l 4: x 2 = 1.

Прямая l 1 проходит через точку с координатами (0;0). Для ее построения выразим x 2 через x 1: x 2 = 4x 1 . Найдем еще одну точку, через которую проходит прямая l 1 , например (1;4). Через точку с координатами (0;0) и точку с координатами (1;4) проведем прямую l 1 .

Для приведения уравнения прямой l 2 к виду в отрезках на осях (2.2.3) разделим обе его части на 6:
. Таким образом, прямаяl 2 отсекает на оси Ох 1 6 единиц, на оси Ох 2 - 2 единицы. Аналогично имеем для l 3:
и Прямаяl 4 параллельна оси Ох 1 и проходит через точку с координатами (0;1) .

Для определения полуплоскостей, которые отвечают ограничениям системы (2.2.4) в ограничения нужно подставить координаты какой-либо точки, не лежащей на граничной прямой. В силу ограничений х 1 0, х 2 0, область допустимых решений ЗЛП лежит в первой четверти координатной плоскости.

О
бласть допустимых решений на рисунке 2.2.2 заштрихована.

Рисунок 2.2.2 – Область допустимых решений

Построим вектор направлений
= (–2,–1). Далее строим линию уровня, перпендикулярно к вектору.

Для нахождения наибольшего значения целевой функции передвигаем линию уровня в направлении вектора до последнего пересечения с областью допустимых решений. Таким образом, точкой максимума целевой функцииz является точкаА (пересечение прямыхl 1 иl 2).

Для вычисления оптимального значения целевой функции z найдем координаты точкиА . Поскольку точкаА – это точка пересечения прямыхl 1 иl 2 , то ее координаты удовлетворяют системе уравнений, составленной из уравнений соответствующих граничных прямых:

Таким образом, точка А имеет координаты x 1 =6/13, x 2 = 24/13.

Подставив координаты точки А в целевую функцию (2.2.5), получим оптимальное значение целевой функции

max z = – 2·(6/13) – (24/13) = – 36/13.

Для нахождения наименьшего значения целевой функции передвигаем линию уровня в направлении, противоположном вектору до последнего пересечения с областью допустимых решений. В этом случае целевая функция неограниченна в области допустимых решений, т.е. ЗЛП минимума не имеет.

В результате решения ЗЛП возможны следующие случаи:

Целевая функция достигает оптимального значения в единственной вершине многоугольника решений;

Целевая функция достигает оптимальное значение в любой точке ребра многоугольника решений (ЗЛП имеет альтернативные опорные планы с одинаковыми значениями z);

ЗЛП не имеет оптимальных планов;

ЗЛП имеет оптимальный план в случае неограниченной области допустимых решений.